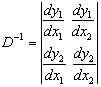23. Прохождение случайных сигналов через нелинейные безинерционные цепи.

       Рассмотрим теперь задачу о прохождении случайного процесса через нелинейную систему. В общем случае эта задача весьма сложная, но она значительно упрощается, когда нелинейная система является безынерционной. В безынерционных нелинейных системах значения выходного процесса  в данный момент времени определяются значениями входного процесса  в тот же самый момент времени. Для нелинейных безынерционных преобразований более простой задачей является определение функций распределения на выходе в гораздо более сложной – определение корреляционной функции или энергетического спектра.

Как отмечалось выше, n - мерная функция распределения случайного процесса по сути дела является функцией распределения n случайных величин, представляющих собой значения случайного процесса в n различных моментов времени, Определение законов распределения функционально преобразованных случайных величин является сравнительно простой задачей.

       Рассмотрим простейший пример одномерной случайной величины. Пусть  - плотность вероятности случайной величины ζ, которая подвергается нелинейному преобразованию . Определим плотность вероятности  случайной величины η. Предположим, что функция  такова, что обратная ей функция  – однозначна.

Если случайная величина ζ находится в достаточно малом интервале , то вследствие однозначной функциональной зависимости между ζ и η случайная величина η обязательно будет находиться в интервале , где , вероятности этих событий должны быть одинаковыми, т.е.            (3.4.13)

откуда находим

                        (3.4.14)

Производная в последнем выражении берется по абсолютной величине, так как плотность вероятности не может быть отрицательной. Если обратная функция  неоднозначная, т.е. имеет несколько ветвей , то для плотности вероятности с использованием теоремы сложения вероятностей можно получить

        (3.4.15)

       Отметим, что для определения числовых характеристик нелинейно-преобразованных случайных процессов нет необходимости определять их плотности вероятностей. Действительно, в общем случае для начального момента  k-го порядка имеем 

           (3.4.16)

Но согласно (3.4.13)  и . Поэтому последнее выражение можно переписать

              (3.4.17)

       Полученные выражения (3.4.14) и (3.4.15) легко распространить на случай нескольких величин. Приведем здесь лишь окончательный результат для двумерного случая. Если случайные величины  и  имеют совместную плотность вероятностей , то для случайных величин

         (3.4.18)

при однозначности обратных функций

           

совместная плотность вероятностей будет определяться выражением

        где величина 

                     

 

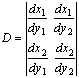
называется якобианом преобразования и представляет собой отношение элементарных площадей  при переходе от одной системы координат к другой. Если , то справедливо равенство

     

где