3.10 Марковские цепи
Последовательность случайных величин 
образует дискретную
цепь Маркова, если для всех n и всех возможных
случайных величин выполняется равенство:
. (3.1)
Если 
, то говорят, что на n -
ом шаге система находится в состоянии 
. Выражение в правой части равенства (1) называют
вероятностью перехода; оно задает условную вероятность перехода из состояния 
на n -1- ом шаге в 
на n - ом шаге.
Обычно цепь Маркова описывается матрицей вероятностей
перехода: 
и вектором 
, где 
– это вектор
начальных вероятностей, показывающий в каком состоянии была система на нулевом шаге,
L – количество состояний цепи Маркова.
и
удовлетворяют условию:
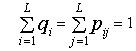. (3.2)
Матрицы, удовлетворяющие условию (3.2) называют стохастическими
Если вероятности перехода не зависят от n (стационарны во времени), то цепь Маркова называется однородной и строгое ее определение задается равенством:
. (3.3)
Для однородной цепи Маркова матрица вероятностей перехода за
m шагов выглядит следующим образом: 
.Цепь Маркова называется неприводимой, если каждое ее состояние может быть достигнуто из любого
другого. Для любой пары 
и существует такое k, что 
.
Обозначим через 
вероятность пребывания
системы на n-ом шаге в
состоянии : 
.
Распределение вероятностей 
называется стационарным, если при его выборе в качестве начального распределения
вероятностей 
, для всех n выполняется
равенство 
.
Состояние Ej называют эргодическим, если оно является апериодическим, возвратным ненулевым, т.е. fj =1, Mj <¥, g = 1. Если все состояния цепи Маркова эргодические, то сама цепь Маркова является эргодической.
Для эргодической цепи Маркова всегда существует стационарное распределение вероятностей состояний системы, не зависящее от начального распределения вероятностей.
