10 Псевдослучайные коды(последовательности)

Наряду с ортогональными кодами важную роль в системах с расширенным спектром играют псевдослучайные последовательности , среди которых наибольшее значение получили:

-М-последовательности

-коды Голда

-коды Кассами

Формированеи М-последовательности осуществляется системой из n-линейных регистров хранения сдвига и K сумматоров по |2|, а так же контура обратной связи. Длина М-последовательности определяется количеством сумматоров и максимально может составить , где:

n- количество регистров хранения сдвига

Максимально достижимое значение автокорреляционной функции:

Рассмотрим в качестве примера по формированию М-последовательности  систему состоящую из n=4 регистров хранения сдвига и к=1 сумматоров по |2|:

 

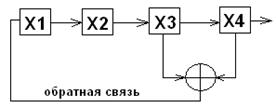
Работа по генерации М- последовательности осуществляется следующим образом:

С каждым новым тактом содержимое регистра сдвигается на одну позицию вправо

Содержимое регистров Х3 и Х4 суммируются по |2|. Результат суммирования по обратной связи подается на входной регистр Х1. Итоговая последовательность –это то. Что формируется на выходе регистра Х4

Пусть в регистрах содержатся следующие двоичные значения:

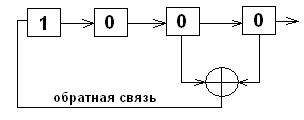
Тогда на выходе регистра Х4 при каждом новом такте будем иметь:

1такт               1000               0

2такт               0100               0

3такт               0010               0        

4такт               1001               1    

5такт               1100               0   

6такт               0110               0     

7такт               1011               1       

8такт               0101               1      

9такт               1010               0   

…………………………………

 

14такт             0011               1         

15такт             0001               1          

16такт             1000               0    

 

Поскольку последнее состояние регистров Х1,Х2,Х3,Х4 идентично первоначальному, то заключаем, что длина полученной последовательности равна 15, что соответствует максимально возможной  длине:    

Таким образом на выходе регистра Х4 мы получим двоичную последовательность вида: 111101011001000.

Проверим данную последовательность на случайность!!!

А) проверка на сбалансированность

Количество «1» -8

Количество «0»-7                    вывод:- сбалансирована

 

Б) Проверка на цикличность:

Количество циклов по  «1» -4

Количество циклов с «0» -4

Итого 8 циклов

При этом  половина из этих циклов(т.е. 4) имеет длину =1

                   1/4  (т.е 2) имеет длину =2

Поскольку последовательность короткая по длине, проверку дальше осуществить не представляется возможным , тем не менее видно, что условие цикличности выполняется

В) Проверка на корреляцию

Сравниваем с первоначальной

Исх: 111101011001000	Число совпадений	Число несовпадений	разница
011110101100100	7	8	-1
001111010110010	7	8	-1
000111101011001	7	8	-1

 И так далее

Это означает, что данная последовательность коррелированна

Т.к все 3 условия выполняются , то данная последовательность является псевдослучайной.

 

Если проанализировать данный пример и схему изображенную на рисунке, то несложно заметить, что длина , характеристики и корреляционные свойства М-последовательности существенно будут зависеть от количества сумматоров и формы организации контура обратной связи. В этом смысле различают «плохие » и «хорошие» М-последовательности, отнеся к последним М-последовательности с высокими значениями автокорреляционной функции. Дальнейшее увеличение автокорреляционной  функции и достижение хороших взаимокорреляционных свойств между кодовыми последовательностями возможно путем комбинации нескольких М-последовательностей. На этом принципе и основаны схемы генерации кодов Голда и  кодов Кассами.

Коды Голда

Формируются на основе 2-х специально подобранных М-последовательностей и их посимвольного сложения по |2|.(смотри следующий рисунок)

Существенным моментом при формировании кодов Голда является использование особых пар М-последовательностей , называемых  предпочтительными (они перечислены в специальной литературе)

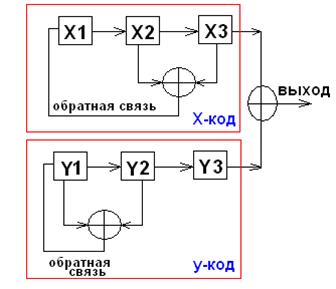
Т.к. обе М-последовательности имеют одну и ту же длину М и тактируются единым генератором , то и формируемая последовательность Голда будет иметь длину равную , где :

n- это количество разрядов регистра сдвига в генераторе отдельно взятой последовательности

Коды Кассами

Реализуются с помощью 3-х последовательно включенных М-последовательностей, которые так же подбираются исходя из критерия предпочтительности с различными обратными  связями:

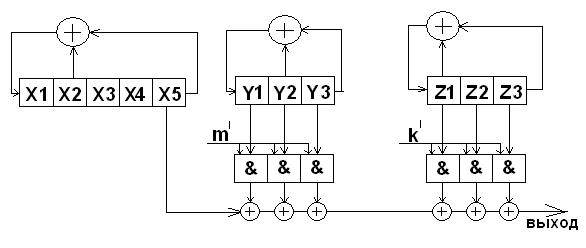
, где m' и k'- циклические сдвиги кодов генерируемых регистрами y и z соответственно

Генераторы кодов кассами с размерностью (n(=5)  m(=3) k(=3)), где n,m,k- число регистров хранения сдвига в генераторах М-последовательности x,y,z соответственно,формируют кодовые последовательности с заданными свойствами только в том случае, если y и z М-последовательности имеют различные относительно друг друга циклические сдвиги задаваемые m' и k'

Семейство кодов Кассами содержит  последовательностей с периодом

Они считаются оптимальными в том  смысле, что для любой пары кодовой последовательности  Кассами обеспечиваются максимальные значения автокорреляционной функции равные: